Recent posts
MathChat - An Conversational Framework to Solve Math Problems
TL;DR:
- We introduce MathChat, a conversational framework leveraging Large Language Models (LLMs), specifically GPT-4, to solve advanced mathematical problems.
- MathChat improves LLM’s performance on challenging math problem-solving, outperforming basic prompting and other strategies by about 6%. The improvement was especially notable in the Algebra category, with a 15% increase in accuracy.
- Despite the advancement, GPT-4 still struggles to solve very challenging math problems, even with effective prompting strategies. Further improvements are needed, such as the development of more specific assistant models or the integration of new tools and prompts.
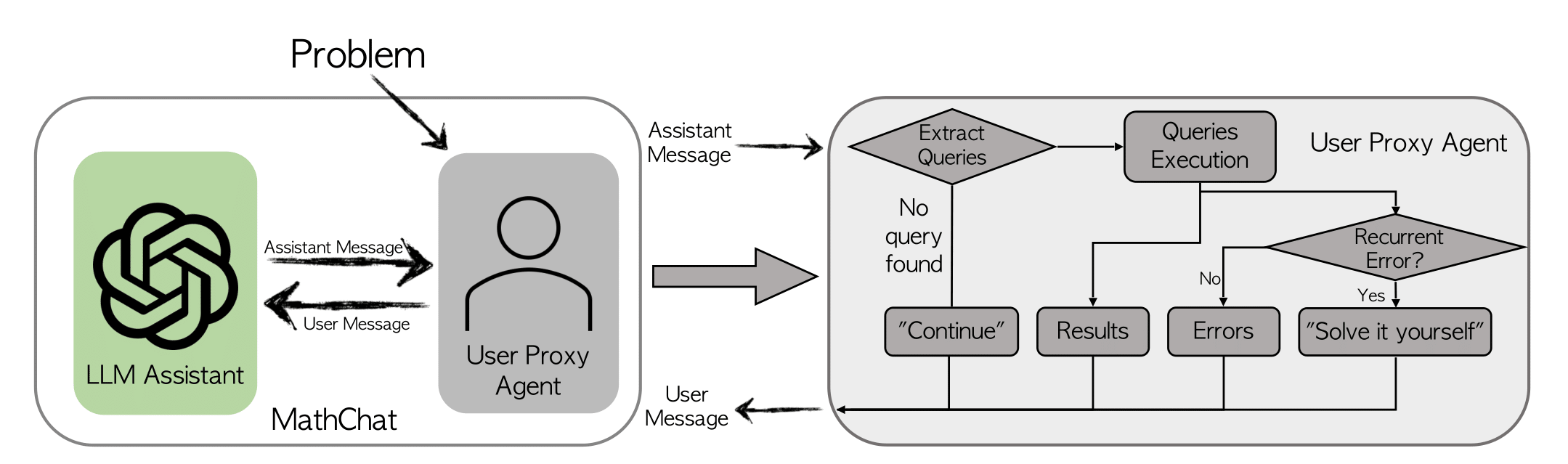
The MathChat Framework
MathChat simulates a conversation between the LLM assistant and a user proxy agent. As the name indicates, the user proxy agent acts as a proxy for the user, which is responsible for communicating with the LLM assistant and continuing the conversation in a desired manner. The proxy agent first presents a math problem to the LLM assistant, framed by an initial prompt that guides the assistant in how it should work collaboratively to solve the problem. We incorporate existing prompting methods such as CoT (chain-of-thought) and tool-using are incorporated in the initial prompt. Key components of the prompt include:- Tool-using Prompt: This guides the LLM assistant to use Python code in the correct format to address the problem, allowing the user proxy agent to parse the code and provide the appropriate results.
-
Problem-Solving Strategy Selection Prompt: The assistant is instructed to choose one of three potential problem-solving strategies, including:
- Writing a Python program to solve the problem directly.
- Solving the problem directly without using Python, which exercises LLMs’ inherent reasoning capabilities.
- Solving the problem step by step with Python. This should be used when the first two strategies aren’t suitable.
- Final Answer Encapsulation Prompt: This part instructs the assistant to put the final answer in \boxed.
| Participant | Dialogue |
|---|---|
| User Proxy Agent | (Initial Prompt: Let’s solve a math problem with Python…) Problem: Find all x that satisfy the inequality (2x+10)(x+3) < (3x+9)(x+8). Express your answer in interval notation. |
| LLM assistant | The key idea to solve this problem is to find the critical points, which are the points where the inequality is equal. Then, test the intervals between the critical points to find the interval for which the inequality holds. |
| LLM assistant (continued) | Here’s Python code to find the critical points: from sympy import symbols, Eq, solve; x = symbols("x"); lhs = (2*x + 10)*(x + 3); rhs = (3*x + 9)*(x + 8); equation = Eq(lhs, rhs); critical_points = solve(equation, x); critical_points |
| User Proxy Agent | The critical points are: [-14, -3] |
| LLM assistant | We found the critical points to be x = -14 and x = -3. Now we’ll test the intervals between these critical points as well as points before and after the critical points. The intervals are: x < -14, -14 < x < -3, x > -3. |
| LLM assistant (continued) | Here’s Python code to test the inequality for each interval: from sympy import symbols; x = symbols("x"); inequality = (2*x + 10)*(x + 3) < (3*x + 9)*(x + 8); test_points = [-15, -5, 0]; intervals = []; for point in test_points: if inequality.subs(x, point): intervals.append(point); intervals |
| User Proxy Agent | The intervals where the inequality holds true are for test points: [-15, 0] |
| LLM assistant | We have tested the intervals and found that the inequality holds for: 1. x < -14 (test point: -15) 2. x > -3 (test point: 0). Therefore, the solution to the inequality (2x+10)(x+3) < (3x+9)(x+8) is x ∈ (-∞, -14) ∪ (-3, ∞) |
Experiment Setup
We evaluate the improvement brought by MathChat. For the experiment, we focus on the level-5 problems from the MATH dataset, which are composed of high school competition problems. These problems include the application of theorems and complex equation derivation and are challenging even for undergraduate students. We evaluate 6 of 7 categories from the dataset (excluding Geometry): Prealgebra, Algebra, Number Theory, Counting and Probability, Intermediate Algebra, and Precalculus. We evaluate GPT-4 and use the default configuration of the OpenAI API. To access the final performance, we manually compare the final answer with the correct answer. For the vanilla prompt, Program Synthesis, and MathChat, we have GPT-4 enclose the final answer in \boxed, and we take the return of the function in PoT as the final answer. We also evaluate the following methods for comparison:- Vanilla prompting: Evaluates GPT-4’s direct problem-solving capability. The prompt used is: ” Solve the problem carefully. Put the final answer in \boxed”.
- Program of Thoughts (PoT): Uses a zero-shot PoT prompt that requests the model to create a Solver function to solve the problem and return the final answer.
- Program Synthesis (PS) prompting: Like PoT, it prompts the model to write a program to solve the problem. The prompt used is: “Write a program that answers the following question: {Problem}”.
Experiment Results
The accuracy on all the problems with difficulty level-5 from different categories of the MATH dataset with different methods is shown below: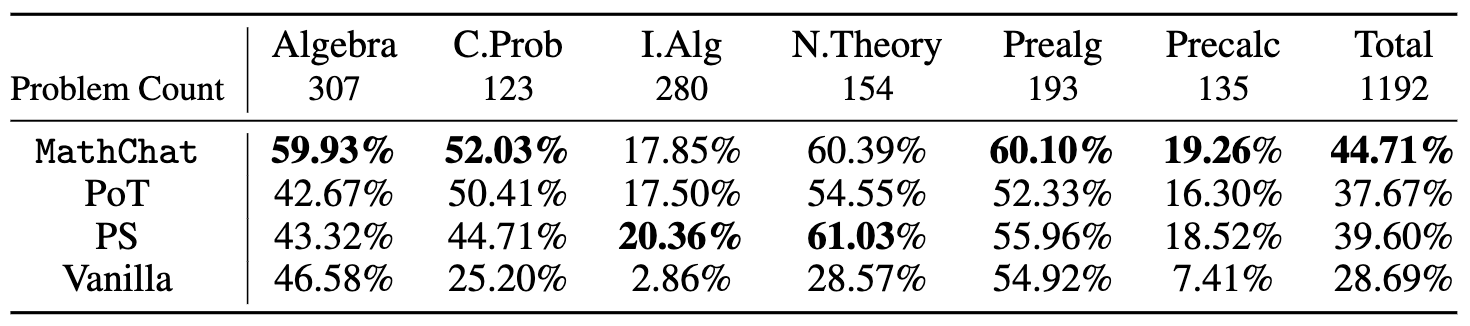
We found that compared to basic prompting, which demonstrates the innate capabilities of GPT-4, utilizing Python within the context of PoT or PS strategy improved the overall accuracy by about 10%. This increase was mostly seen in categories involving more numerical manipulations, such as Counting & Probability and Number Theory, and in more complex categories like Intermediate Algebra and Precalculus.
For categories like Algebra and Prealgebra, PoT and PS showed little improvement, and in some instances, even led to a decrease in accuracy. However, MathChat was able to enhance total accuracy by around 6% compared to PoT and PS, showing competitive performance across all categories. Remarkably, MathChat improved accuracy in the Algebra category by about 15% over other methods. Note that categories like Intermediate Algebra and Precalculus remained challenging for all methods, with only about 20% of problems solved accurately.
The code for experiments can be found at this repository.
We now provide an implementation of MathChat using the interactive agents in AutoGen. See this notebook for example usage.
Future Directions
Despite MathChat’s improvements over previous methods, the results show that complex math problem is still challenging for recent powerful LLMs, like GPT-4, even with help from external tools. Further work can be done to enhance this framework or math problem-solving in general:- Although enabling the model to use tools like Python can reduce calculation errors, LLMs are still prone to logic errors. Methods like self-consistency (Sample several solutions and take a major vote on the final answer), or self-verification (use another LLM instance to check whether an answer is correct) might improve the performance.
- Sometimes, whether the LLM can solve the problem depends on the plan it uses. Some plans require less computation and logical reasoning, leaving less room for mistakes.
- MathChat has the potential to be adapted into a copilot system, which could assist users with math problems. This system could allow users to be more involved in the problem-solving process, potentially enhancing learning.